我们来玩个游戏,假设你有一个飞镖靶(圆形)和一个同等大小的飞镖贴,把飞镖贴贴在飞镖靶上,然后开始玩飞镖,规则如下:
假设你有一个能让飞镖射出去后能保持在飞镖靶上的特异功能,即飞镖的落点总是在飞镖靶内。
你是一个机器人,做出的行动总是随机的,因此,飞镖落在飞镖靶内的概率是同等的。
飞镖射出去以后,如果它的落点在飞镖贴上的话,以落点到圆心的距离为半径画圆,剪去飞镖上画出的圆外的贴纸,只留下画出的圆,将它作为新的飞镖贴,开始下一轮游戏
如果飞镖落在飞镖贴外,结束游戏,此时飞镖靶上的飞镖个数即为所得分数
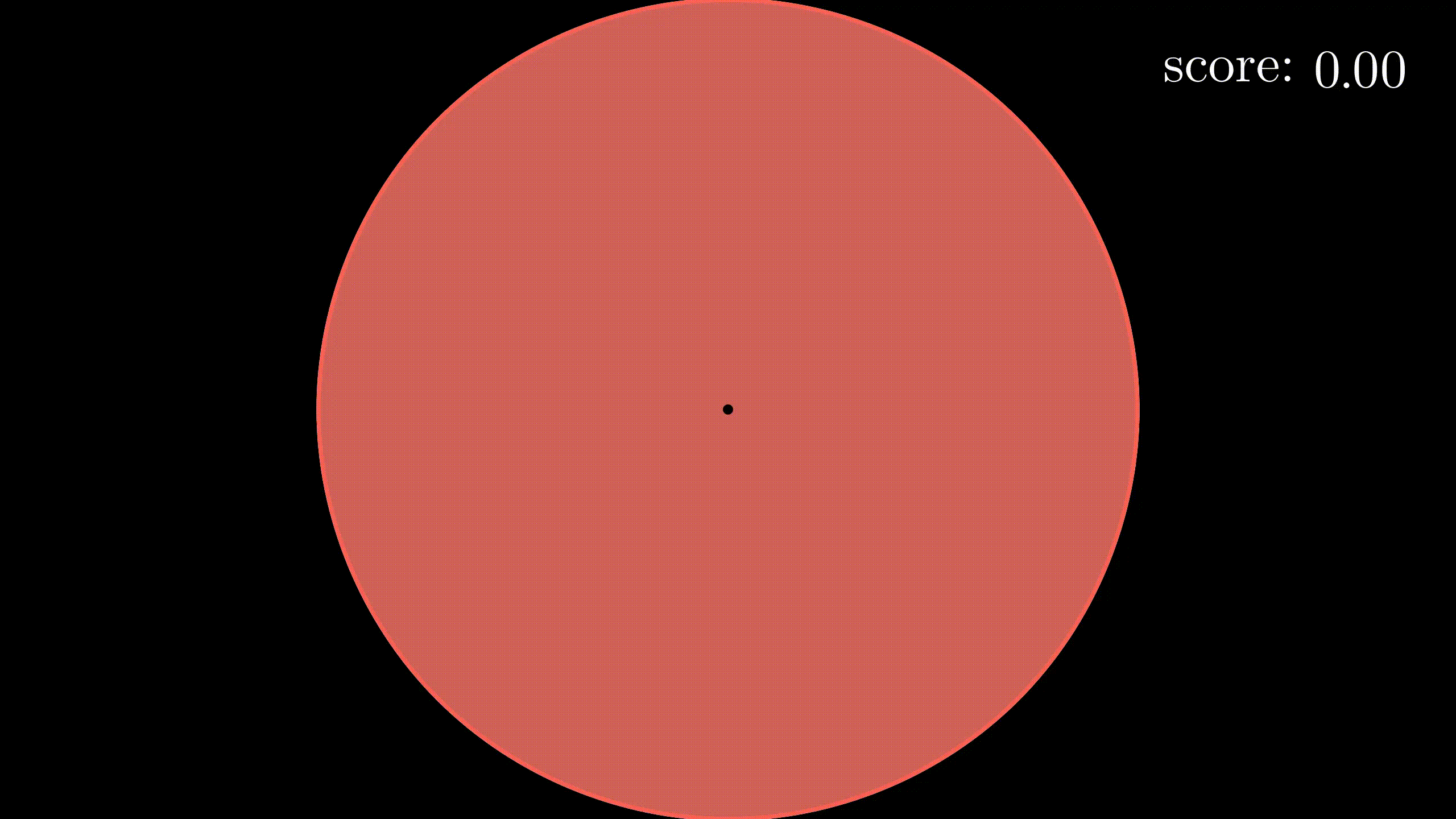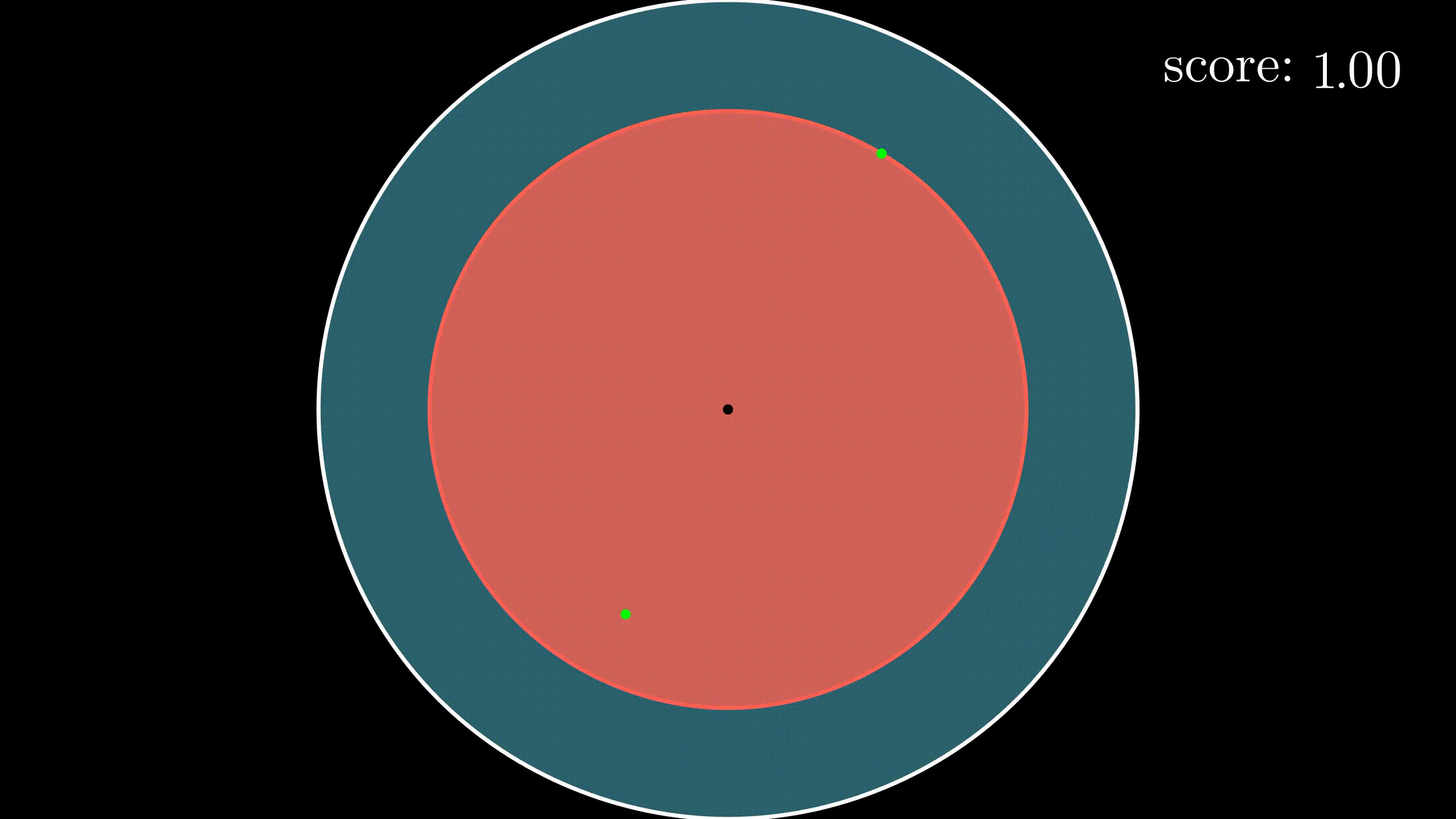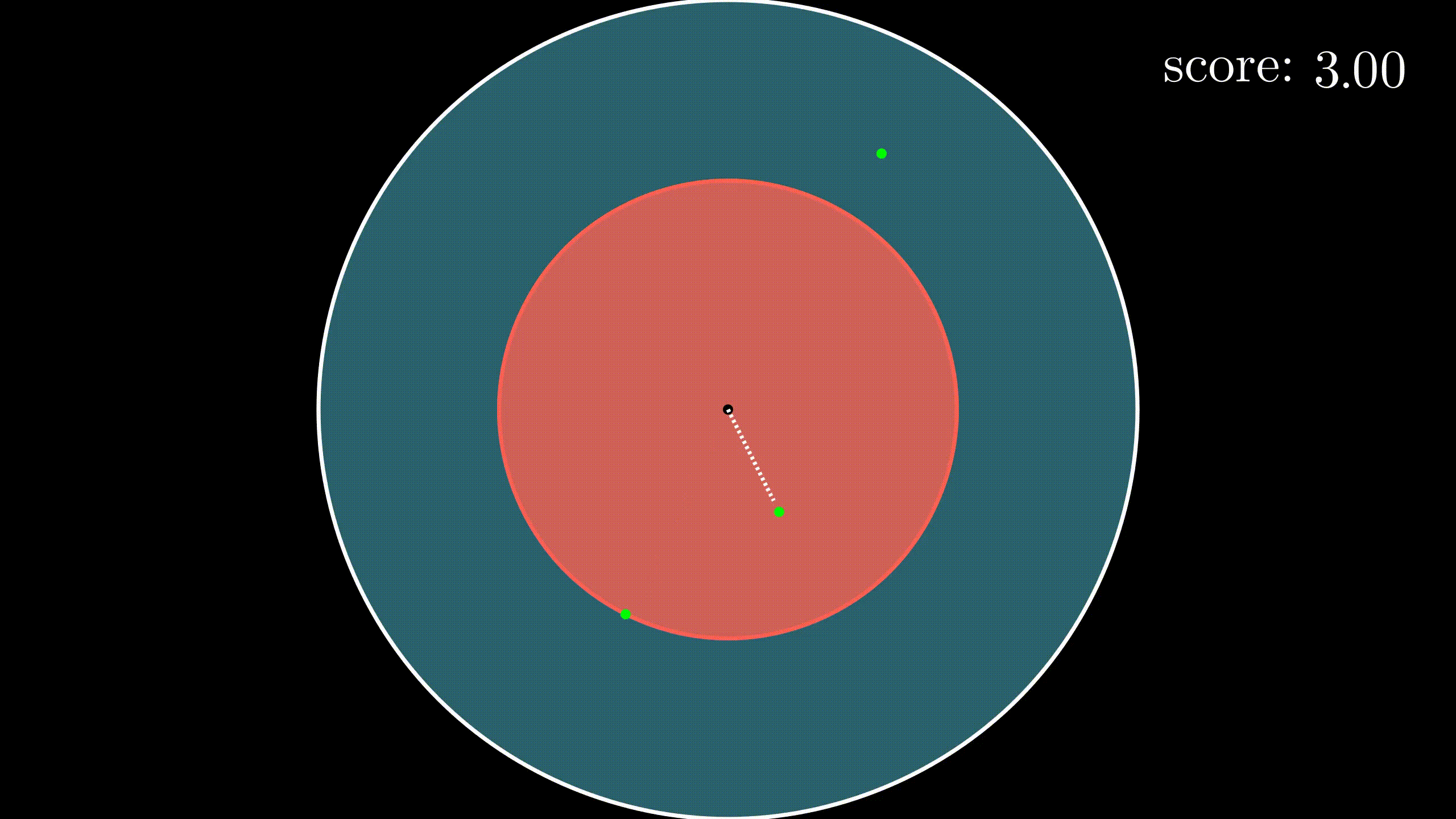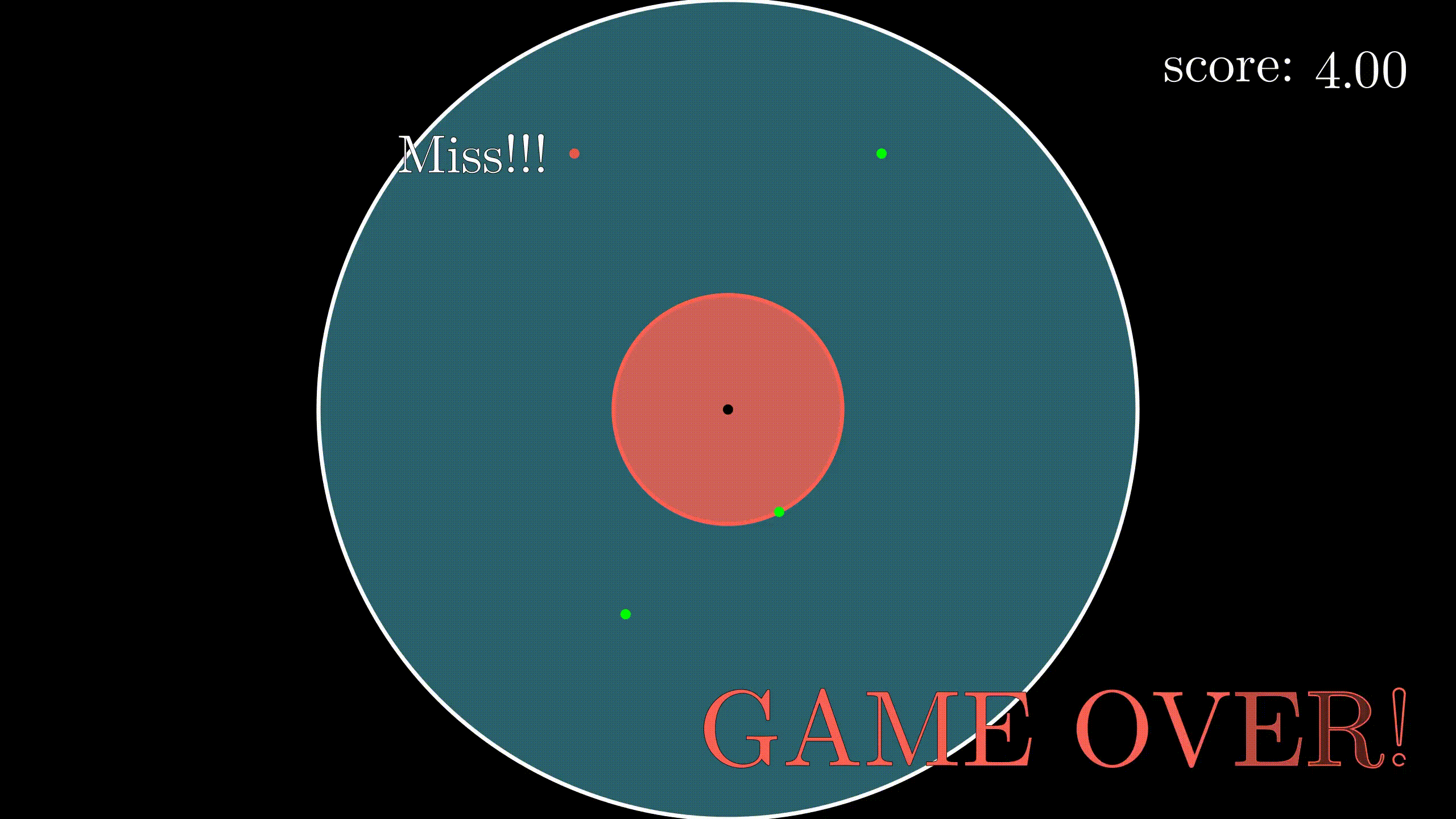
如果还不明白的话,整个动画应该就明白了吧。蓝色的大圆盘就是我们的飞镖靶,红色的就是飞镖贴,哪些红红绿绿的小点点就是我们飞镖的落点,右上角是我们的得分。可以看到这局游戏的最后我们的得分是4,因为最后一共有4个点落在飞镖靶上,尽管最后一个飞镖打在了飞镖贴外,但这一个依然算在内。你可以看出,游戏会越来越难。
我给你的问题就是求出所得分数的期望值。一个很好的思路就是把分数为n的概率乘以n然后对其求和,即下面这条式子:
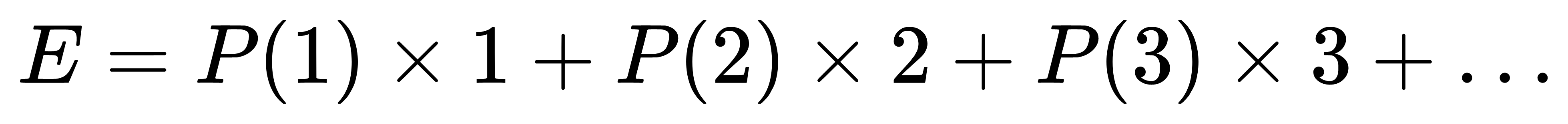
啊,又要埋坑,随缘更新啊?那没事了(滑稽)
大家可以一起来讨论一下,猜一下答案什么的。
小提示:这个问题很有实际意义(仅仅是意义),在自然界中,这种现象也不少见,生物的繁衍生息,石头年龄的变化,时间...都离不开它。
最后于 2021-7-15
被皮蒂亚编辑
,原因:
高三力。。